[latexpage]
วันนี้ เราจะมาทำความรู้จักกับกลไกสำหรับการปกป้องความลับของข้อมูลส่วนบุคคลด้วย Differential Privacy
โดยหลักการของ differential privacy คือการเพิ่มสิ่งรบกวนทางคณิตศาสตร์ (noise) เข้าไปในข้อมูลเพื่อไม่ให้สามารถบ่งชี้ตัวตนของบุคคลได้ ซึ่งวิธีที่ง่ายที่สุดในการปกป้องความเป็นส่วนบุคคล คือการละเว้นข้อมูลทั้งหมดที่สามารถนำไปประกอบชี้ตัวตนบุคคลได้ เช่น ชื่อ นามสกุล อายุ เพศ วันเดือนปีเกิด ฯลฯ แต่โดยส่วนใหญ่แล้ว วิธีดังกล่าวจะทำให้เสียข้อมูลและอาจจะทำให้ไม่สามารถนำชุดข้อมูลไปใช้ต่อได้เลย
ซึ่งเคล็ดลับของ differential privacy คือการเพิ่ม noise ด้วยหลักการทางคณิตศาสตร์
โดยสามารถชี้วัดได้ว่า
- ข้อมูลตัวตนบุคคลยังคงเป็นความลับอยู่มากเท่าไร
- ข้อมูลยังมีคุณสมบัติเดิมอยู่มากเท่าไร และ
- ผลการวิเคราะห์ยังคงมีความถูกต้องอยู่มากเท่าไร
การประกาศผลสถิติสามารถเปิดเผยข้อมูลส่วนบุคคลได้
คุณเคยคิดบ้างไหมว่า การประกาศผลสถิติไม่ได้เปิดเผยข้อมูลส่วนบุคคลใด ๆ
แต่ในความเป็นจริง ใคร ๆ หรือสาธารณะอาจจะรู้มากกว่าที่คุณคิดได้ ในบทความนี้ เราจะมาทำความเข้าใจกันว่า เราจะต้องทำอย่างไร เพื่อไม่ให้การประกาศผลการวิเคราะห์ใด ๆ เปิดเผยข้อมูลส่วนบุคคลในชุดข้อมูลของเรา
เรามาดูตัวอย่างง่ายๆ กันครับ สมมุติว่าเรามีชุดข้อมูลน้ำหนักของผู้ป่วยจากข้อมูลประวัติการรักษาพยาบาลในตารางที่ 1 ด้านล่าง และเราได้ทำการวิเคราะห์สุขภาพประชาชนไทยโดยคำนวนค่าเฉลี่ยน้ำหนัก และประกาศผลให้เป็นข้อมูลสาธารณะ
| ชื่อ | น้ำหนัก |
|---|---|
| Anand | 60 |
| Ben | 70 |
| Champ | 80 |
| Dao | 40 |
ค่าเฉลี่ยน้ำหนัก : 62.5
โดยข้อมูลในตารางถือว่าเป็นข้อมูลส่วนบุคคล และค่าเฉลี่ยน้ำหนักเป็นข้อมูลสาธารณะ ถ้าคุณ Anand Ben และคุณ Champ เปิดเผยข้อมูลตนเอง เราสามารถคำนวนน้ำหนักของคุณ Dao ($x$) จากค่าเฉลี่ยได้ โดย
\begin{align*}
\frac{60 + 70 + 70 + x}{4} &= 62.5\\
x &= 40
\end{align*}
ทั้งนี้ คุณ Dao ไม่ได้ยินยอมหรือมีความประสงค์ที่จะเปิดเผยข้อมูลส่วนตัวของตนเองให้เป็นสาธารณะ ดังนั้น การประกาศค่าเฉลี่่ยน้ำหนักในครั้งนี้ จึงเป็นการละเมิดความลับข้อมูลส่วนบุคคลของคุณ Dao
เราอยากที่จะประกาศผลการวิเคราะห์หรือค่าเฉลี่ยโดยที่สาธารณะไม่สามารถทราบน้ำหนักของคุณ Dao ได้ แม้กระทั่งมีการเปิดเผยข้อมูลใด ๆ เพราะฉะนั้น สาธารณะจะไม่สามารถแยกตารางชุดข้อมูลจริงออกจากตารางชุดข้อมูลปลอมได้ เช่น ถ้าค่าเฉลี่ยน้ำหนักที่เราประกาศคือ 63.75 และมีชุดข้อมูลในตารางที่ 2 ซึ่งแตกต่างจากตารางที่ 1 ที่ค่าน้ำหนักของคุณ Dao จุดเดียว
| ชื่อ | น้ำหนัก |
|---|---|
| Anand | 60 |
| Ben | 70 |
| Champ | 80 |
| Dao | 50 |
สาธารณะจะไม่สามารถทราบได้ว่า ค่าเฉลี่ยดังกล่าวเป็นของตารางที่ 1 หรือ 2 เพราะค่าเฉลี่ยที่ประกาศจะไม่ตรงกับค่าเฉลี่ยที่คำนวนได้จากทั้งสองตาราง เราจึงเรียกสองตารางที่แตกต่างจากกันเพียงค่าเดียวว่า Neighbors ซึ่งเป็นคุณสมบัติสำคัญของตารางชุดข้อมูลสำหรับการนิยามของ differential privacy
เราจะเห็นได้ว่าค่าน้ำหนักเฉลี่ย 63.75 ขาดความถูกต้อง เพราะค่าดังกล่าว ไม่ตรงกับค่าเฉลี่ยที่สามารถคำนวนได้จากทั้ง 2 ตาราง โดยการประกาศค่าเฉลี่ยน้ำหนักเป็น 63 จะทำให้ผลการวิเคราะห์มีความถูกต้องมากขึ้นหากข้อมูลจริงคือข้อมูลในตารางที่ 1 เพราะค่าเฉลี่ยที่ประกาศไปใกล้เคียงกับค่าเฉลี่ยของตารางที่ 1 มากกว่าตารางที่ 2 แต่ในขณะเดียวกัน สาธารณะจะมีความมั่นใจมากขึ้นว่า น้ำหนักของคุณ Dao ใกล้ 40 มากกว่า 50 ดังนั้น การคุ้มครองและปกป้องข้อมูลส่วนบุคคลในกรณีนี้ จึงมี tradeoff ระหว่างความถูกต้องของผลการวิเคราะห์และความลับของข้อมูลส่วนบุคคล
Differential Privacy และ Laplace Mechanism
เป้าหมายของการทำ differential privacy คือการทำให้สาธารณะไม่สามารถแยกตารางใด ๆ ก็ตามที่เป็น neighbors ออกจากกันได้ โดยหลักการในทางคณิตศาสตร์คือการเพิ่ม noise เข้าไปในผลการวิเคราะห์ ($\alpha$)
\begin{equation}
\text{Average Weight} = \frac{\sum_{n=1}^{N}W_n}{N} + \alpha
\label{eq:average}
\end{equation}
โดย $W_n$ คือน้ำหนักของแต่ละบุคคล และ $N$ คือจำนวนบุคคลทั้งหมด
การเลือก $\alpha$ มีอยู่หลายวิธี วิธีพื้นฐานสำหรับค่าที่เป็นตัวเลขคือ Laplace mechanism
Laplace mechanism คือการสุ่มค่า noise จาก Laplacian distribution ซึ่งมีลักษณะต่อไปนี้
\begin{equation}
Lap\left ( b \right ) = p\left ( x; b \right ) = \frac{1}{2b}e^{-\frac{|x-\mu|}{b}}
\label{eq:laplace}
\end{equation}
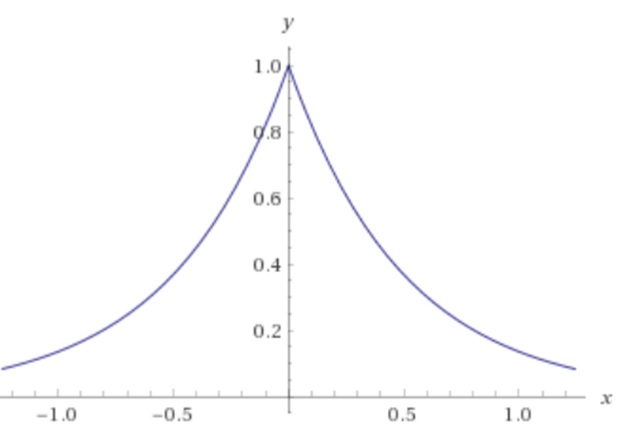
ตัวอย่างของ Laplace distribution จะอยู่ในรูปที่ 1

โดยปกติในการสุ่มค่า noise เราจะเลือก $\mu$ ให้เท่ากับ 0 เมื่อ $\mu$ เท่ากับ 0 ค่าคาดหมายจึงเท่ากับ 0 และค่าความแปรปรวนจึงเท่ากับ $2b^2$ เพราะฉะนั้น ถ้าค่าของ $b$ ยิ่งสูง โอกาสที่เราจะดึงค่าที่ใหญ่สำหรับค่าของ noise ก็จะสูงขึ้นด้วย
เราสามารถนิยามตัวชี้วัด differential privacy และหา bound ของ noise ได้ โดยเราจำเป็นจะต้องนิยามความแตกต่างในผลการวิเคราะห์สถิติที่มากที่สุดจากบรรดาสองตารางที่เป็น neighbors ทั้งหมดก่อน
\begin{equation}
GS\left ( f\right ) := max_{T,T':\text{neighboring tables}} |f\left ( T \right ) – f\left ( T' \right )|
\label{eq:gs}
\end{equation}
โดย $f\left ( \cdot \right )$ คือผลการวิเคราะห์สถิติ ซึ่งคือค่าเฉลี่ยน้ำหนักในตัวอย่างที่กล่าวไว้เบื่องต้น $T$ และ $T'$ คือตารางที่เป็น neighbors
เมื่อเรารวมทั้งสามสมการด้านบน เราจะได้สมการสำหรับการหา noise ด้วย Laplace mechanism ผลการวิเคราะห์สถิติที่เราประกาศให้สาธารณะ ($y$) สำหรับตารางที่เราสนใจจึงมีรูปแบบในสามการ (\ref{eq:private})
\begin{equation}
y = f\left ( T \right ) + Lap\left [ \frac{GS\left ( f \right )}{\varepsilon } \right ]
\label{eq:private}
\end{equation}
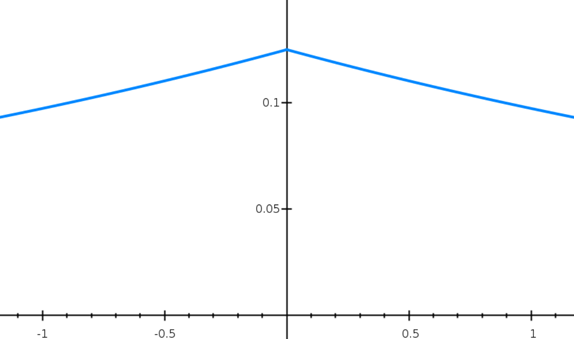
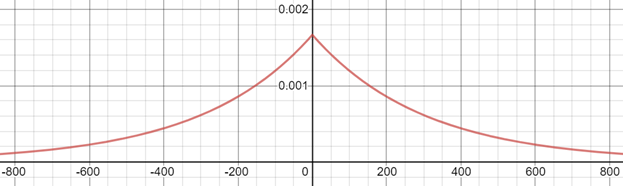
โดย $\varepsilon$ เป็นตัวแปรที่มีค่าระหว่าง 0 กับ 1 จากสมการ (\ref{eq:private}) เมื่อค่าของ $\varepsilon$ ใกล้ 1 การแจกแจงของค่า noise จะยิ่งแคบ (รูปที่ 2) และทำให้โอกาสที่จะสุ่มค่า noise ที่เล็กมากขึ้น ในทางกลับกัน ถ้าค่าของ $\varepsilon$ ใกล้ 0 การแจกแจงของค่า noise จะยิ่งกว้าง (รูปที่ 3) และทำให้มีโอกาสมากขึ้นที่ค่า noise ใหญ่
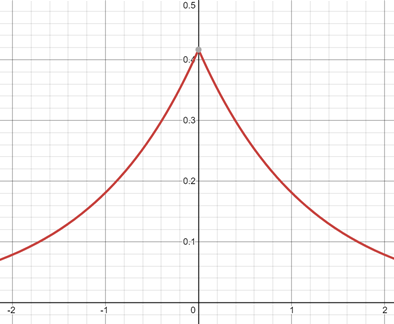
โดยทั่วไป ผู้ใหญ่จะหนักระหว่าง 30 และ 150 กิโลกรัม ซึ่งความแตกต่างที่มากที่สุดในสองตารางที่เป็น neighbors จึงเท่ากับ 150 – 30 หรือ 120 กิโลกรัมโดยประมาณ เพราะฉะนั้น ความแตกต่างในผลการวิเคราะห์สถิติ (ค่าเฉลี่ย) ที่มากที่สุด จึงเท่ากับ $\frac{120}{4}$ จากตัวอย่างชุดข้อมูลที่มีอยู่ 4 คน ดังนั้น ด้วยค่าของ $\varepsilon$ ที่เท่ากับ 0.1 noise จะถูกสุ่มมาจาก $Lap\left [ \frac{30}{0.1} \right ] = Lap\left [ 300 \right ]$ ซึ่งมีลักษณะในรูปที่ 4 ค่าของ noise จึงมีโอกาสที่จะใหญ่มากและทำให้ผลวิเคราะห์ผิดไปจากความเป็นจริงมาก แต่เมื่อชุดข้อมูลเป็น big data และมีข้อมูลของคนจำนวนมาก ค่าของ noise จะเล็กลง โดยถ้าเรามีข้อมูลน้ำหนัก 1,000 คน ค่าของ noise จะถูกสุ่มมาจาก $Lap\left [ \frac{\frac{120}{1000}}{0.1}\right ] = Lap\left [ 1.2 \right ]$ ซึ่งมีลักษณะในรูปที่ 5
เราสามารถหา bound ของ noise จาก Laplace mechanism โดยการอ้างอิง Chebyshev’s Inequality ซึ่งจำกัดโอกาสและความห่างของค่าสุ่มจากค่าคาดหมาย
\begin{equation}
\textup{Pr}\left [|\mathbf{X} – E\left [ \mathbf{X} \right ]| \geq \ksigma \right ]\leq \frac{1}{k^2}
\label{eq:cheby}
\end{equation}
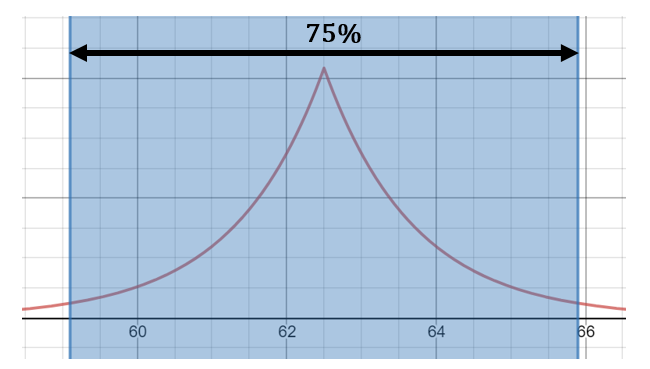
โดย $\mathbf{X}$ คือค่าสุ่ม และ $\sigma$ คือค่าเบี่ยงเบนมาตรฐาน สำหรับตัวอย่างข้อมูลน้ำหนัก 1,000 คน ซึ่งค่าคาดหมายของ noise เท่ากับ 0 และค่าเบี่ยงเบนมาตรฐานสามารถคำนวณจากรากที่สองของค่าความแปรปรวนซึ่งเท่ากับ $\sqrt{2}b=\sqrt{2}\times 1.2\approx 1.7$ ดังนั้น โอกาสที่ค่า noise น้อยกว่า 3.4 (2 เท่าของค่าเบี่ยงเบนมาตรฐาน หรือ $k=2$) จึงมากกว่าหรือเท่ากับ 75% ซึ่งถ้าค่าเฉลี่ยน้ำหนักเท่ากับ 62.5 กิโลกรัม ค่าเฉลี่ยที่ประกาศจะมีค่าระหว่าง 59.1 และ 65.9 กิโลกรัม ด้วยโอกาส 75%
ทั้งนี้ เราสามารถนิยาม $\varepsilon$ – differential privacy และพิสูจน์ว่า Laplace mechanism มีความเป็น $\varepsilon$ – differential private ซึ่งคือคุณสมบัติ
\begin{equation}
e^{-\varepsilon}\leq \frac{\textup{Pr}\left [ out\left ( T \right ) = y \right ]}{\textup{Pr}\left [ out\left ( T' \right ) = y \right ]}\leq e^\varepsilon
\label{eq:diff}
\end{equation}
โดย $y$ คือค่าสุ่มที่เป็นไปได้ทั้งหมด $T$ และ $T'$ คือสองตารางที่เป็น neighbors และ $out\left ( \cdot \right )$ คือผลที่ได้จากกระบวนการทำ differential privacy ซึ่งสามารถตีความสมการ (\ref{eq:diff}) ได้ว่า การเดาว่าผลการวิเคราะห์ $y$ มาจากตาราง $T$ หรือ $T'$ เป็นสิ่งที่ยาก
จากค่า $y$ ค่าของ noise จึงเท่ากับ $y-f\left ( T \right )$ ด้วยความน่าเป็นไปได้ $p\left ( y-f\left ( T \right ); b \right ) = \frac{1}{2b}e^{-\frac{|x-f\left ( T \right )|}{b}}$ โดย $b=\frac{GS\left ( f \right )}{\varepsilon}$ เราจึงสามารถเขียน
$\textup{Pr} \left [ out\left ( T \right ) = y \right ] = \frac{\varepsilon} {2GS\left ( f \right ) }e^{-\varepsilon \frac{|y-f\left ( T \right )|}{GS\left ( f \right )}}$
และ
$\textup{Pr} \left [ out\left ( T' \right ) = y \right ] = \frac{\varepsilon} {2GS\left ( f \right ) }e^{-\varepsilon \frac{|y-f\left ( T' \right )|}{GS\left ( f \right )}}$
เพราะฉะนั้น
\begin{align*}
\frac{\textup{Pr} \left [ out\left ( T \right ) = y \right ]}{\textup{Pr} \left [ out\left ( T' \right )= y \right ]} &= \frac{\frac{\varepsilon} {2GS\left ( f \right ) }e^{-\varepsilon \frac{|y-f\left ( T \right )|}{GS\left ( f \right )}}}{\frac{\varepsilon} {2GS\left ( f \right ) }e^{-\varepsilon \frac{|y-f\left ( T' \right )|}{GS\left ( f \right )}}}\\
&= \frac{\cancel{\frac{\varepsilon} {2GS\left ( f \right )} }e^{-\varepsilon \frac{|y-f\left ( T \right )|}{GS\left ( f \right )}}}{\cancel{\frac{\varepsilon} {2GS\left ( f \right ) }}e^{-\varepsilon \frac{|y-f\left ( T' \right )|}{GS\left ( f \right )}}}\\
&= e^{-\varepsilon \frac{|y-f\left ( T \right )|} {GS \left ( f \right )} + \varepsilon \frac{|y-f\left ( T' \right )|} {GS \left ( f \right )} }\\
&= e^{\frac{\varepsilon}{GS\left ( f \right )}\left ( -|y-f\left ( T \right )| + |y – f\left ( T' \right )| \right )}
\end{align*}
ด้วย Reverse Triangle Inequality
$|p|-|q| \leq |p-q| \label{eq:triangle}$
เราจึงได้
\begin{align*}
\frac{\textup{Pr} \left [ out\left ( T \right ) = y \right ]}{\textup{Pr} \left [ out\left ( T' \right )= y \right ]} &= e^{\frac{\varepsilon}{GS\left ( f \right )}\left ( |y – f\left ( T' \right )| -|y-f\left ( T \right )| \right ) }\\
&\leq e^{\frac{\varepsilon}{GS\left ( f \right )}\left ( |\cancel{y} – f\left ( T' \right ) \cancel{-y}+f\left ( T \right )| \right ) }\\
&= e^{\frac{\varepsilon}{GS\left ( f \right )}\left ( f\left ( T \right ) – f\left ( T' \right )| \right ) }
\end{align*}
และจากนิยามในสมการ (\ref{eq:gs})
$|f\left ( T \right ) – f\left ( T' \right ) | \leq max_{T,T':\text{neighboring tables}} |f\left ( T \right ) – f\left ( T' \right )| = GS\left ( f \right )$
ดังนั้น
\begin{align*}
\frac{\textup{Pr} \left [ out\left ( T \right ) = y \right ]}{\textup{Pr} \left [ out\left ( T' \right ) = y \right ]} &\leq e^{\frac{\varepsilon}{\cancel{GS\left ( f \right )}}\cancel{GS\left ( f \right )}}\\
\frac{\textup{Pr} \left [ out\left ( T \right ) = y \right ]}{\textup{Pr} \left [ out\left ( T' \right )= y \right ]} &\leq e^\varepsilon
\end{align*}
ด้วยวิธีพิสูจน์เดียวกัน
$\frac{\textup{Pr} \left [ out\left ( T \right ) = y \right ]}{\textup{Pr} \left [ out\left ( T' \right )= y \right ]} \geq e^{-\varepsilon}$
$\blacksquare$
Laplace mechanism จึงมีความเป็น $\varepsilon$ – differential private
ข้อสรุป
ค่าของ $\varepsilon$ ในสมการ (\ref{eq:diff}) จึงเป็นตัวชี้วัด differential privacy ที่
- วัดความยากในการนำข้อมูลผลการวิเคราะห์สถิติไปชี้ตัวตนบุคคล
- วัดความแตกต่างของข้อมูลจากข้อมูลเดิม และ
- วัดความถูกต้องของการวิเคราะห์
การเลือกค่า ε ที่ใหญ่จะทำให้ผลการวิเคราะห์มีความถูกต้องมากขึ้น แต่ในขณะเดียวกัน จะทำให้การชี้ตัวตนบุคคลได้ง่ายขึ้นด้วย ดังนั้นการเลือกค่าของ ε จึงต้องมีการประเมินความเสี่ยง ในมุมมองของข้อมูล big data การเพิ่ม noise ด้วยค่าของ ε ที่ต่ำโดยปกติ จะมีผลกระทบต่อความถูกต้องของผลการวิเคราะห์น้อยเพราะข้อมูลมีปริมาณเยอะ เราจึงสามารถใช้ประโยชน์ของ differential privacy ได้อย่างมากเลยทีเดียวครับ
แหล่งที่มาของข้อมูล
C. Dwork and A. Roth. The Algorithmic Foundations of Differential Privacy, Foundation and Trends in Theoretical Computer Science, Vol. 9, Nos. 3-4, pages 211-407, 2014.
V. Suppakitpaisarn. Differential Privacy: Definitions, Laplace Mechanism, Algorithms for Information Security and Privacy, 2018.
อ่านต่อเกี่ยวกับการปกป้องข้อมูลส่วนบุคคลด้วย การพัฒนา AI ด้วยข้อมูลส่วนบุคคล โดยหลักการของ Federated Learning
เนื้อหาโดย เบญจ์ รักตันติโชค
ปรับปรุงและแก้ไขโดย ภคภูมิ สารพัฒน์ และ ปพจน์ ธรรมเจริญพร
Vice President Research and Innovations Division (RIN)
Big Data Institute (Public Organization), BDI
- Ben Ruktantichokehttps://bdi.or.th/author/ben-ru/
- Ben Ruktantichokehttps://bdi.or.th/author/ben-ru/25 มิถุนายน 2020
Data Scientist
Government Big Data Institute (GBDi)
- Pakhapoom Sarapat, PhDhttps://bdi.or.th/author/pakhapoom/28 มิถุนายน 2021
- Pakhapoom Sarapat, PhDhttps://bdi.or.th/author/pakhapoom/10 พฤษภาคม 2021
- Pakhapoom Sarapat, PhDhttps://bdi.or.th/author/pakhapoom/3 พฤษภาคม 2021
Former-Editor-in-Chief at BigData.go.th and Senior Data Scientist at Government Big Data Institute (GBDi )
- Papoj Thamjaroenpornhttps://bdi.or.th/author/papoj/13 ตุลาคม 2023
- Papoj Thamjaroenpornhttps://bdi.or.th/author/papoj/17 สิงหาคม 2023
- Papoj Thamjaroenpornhttps://bdi.or.th/author/papoj/
- Papoj Thamjaroenpornhttps://bdi.or.th/author/papoj/




















